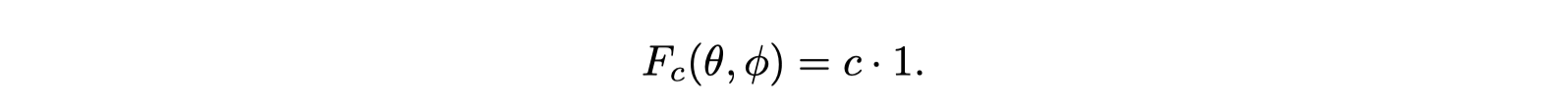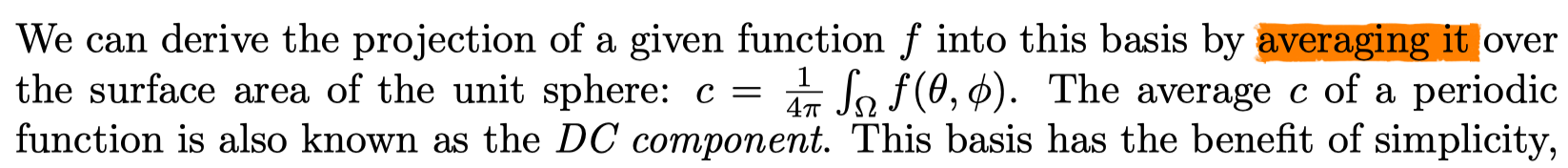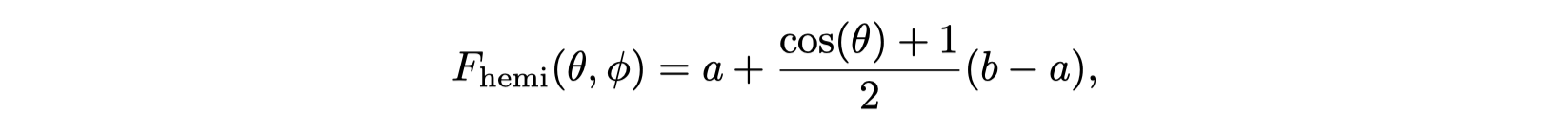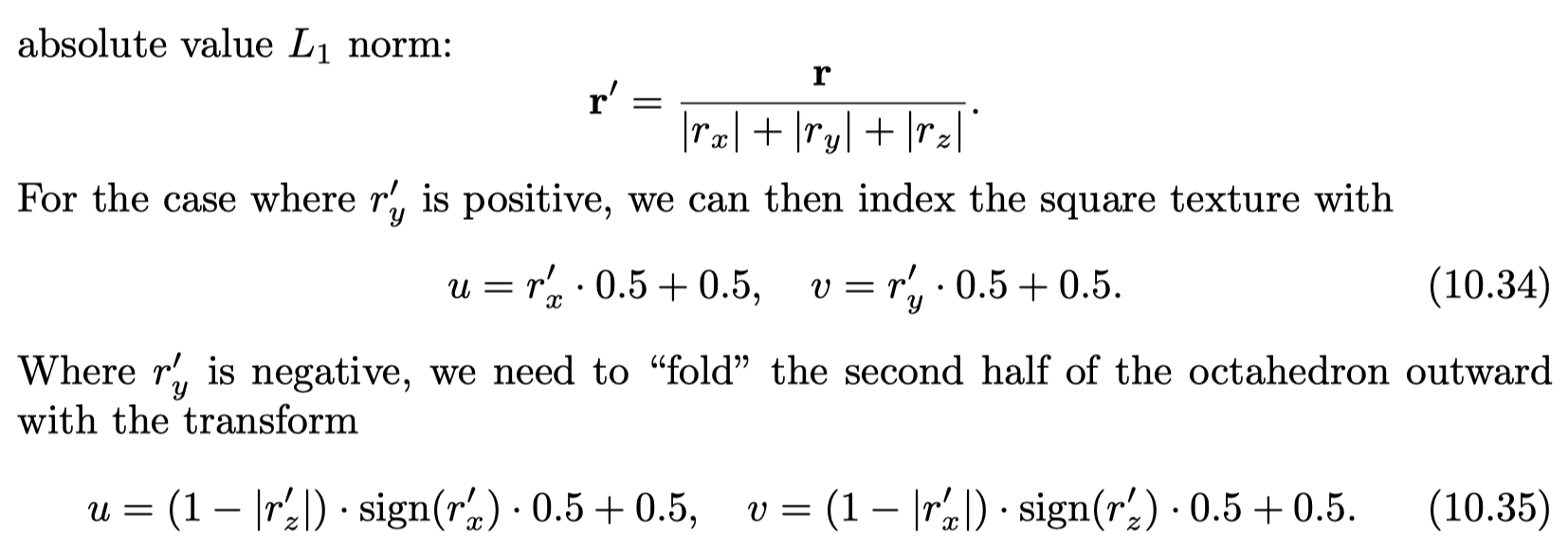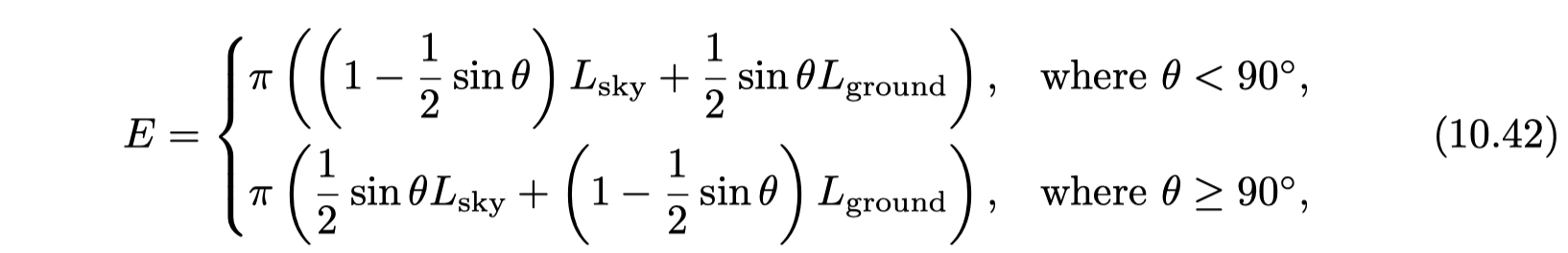Real-Time Local Illumination Summary

Background
Area Light Sources
- Glossy Materials
  - Mittring’s roughness modiﬁcation
  - Representative Point Technique
- General Light Shapes
Environment Lighting
- Ambient Light
Spherical and Hemispherical Functions
Environment Mapping
Specular Image-Based Lighting
- Ideas
- Preﬁltered Environment Mapping
Irradiance Environment Mapping
- Spherical Harmonics Irradiance
- Other Representations
Sources of Error

Background

In reality, lighting is never punctual.
The sky is an important source of light, caused by sunlight scattering from the atmosphere.
In order to form a more realistic lighting model, we need to integrate the BRDF response over the full hemisphere of incident directions on the surface.
In offline rendering, usually averaging multiple samples(rays)
In real-time rendering, we will need to approximate the light emitter, the BRDF, or both.

Area Light Sources

Vector Radiance
Wrap Lighting
Glossy Materials
uniformly emitting spherical area lights and arbitrary glossy BRDFs
Mittring’s roughness modiﬁcation
Mittring, Martin, “The Technology Behind the ‘Unreal Engine 4 Elemental Demo’,” Game Developers Conference, Mar. 2012.
Approximate the convolution between the light source and the material BRDF by ﬁnding a new BRDF lobe, of a diﬀerent roughness, that has a corresponding cone whose solid angle is equal to the sum of the light lobe angle and the material one.
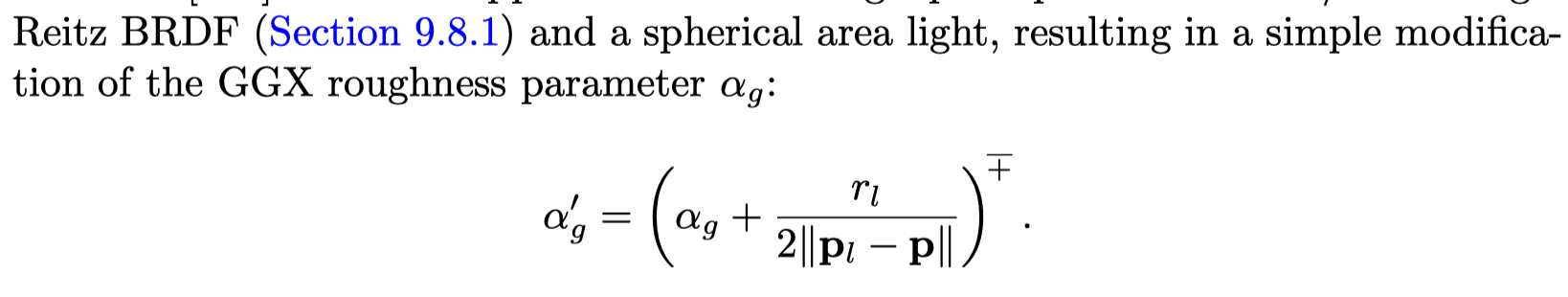
roughness clamp cause artifacts

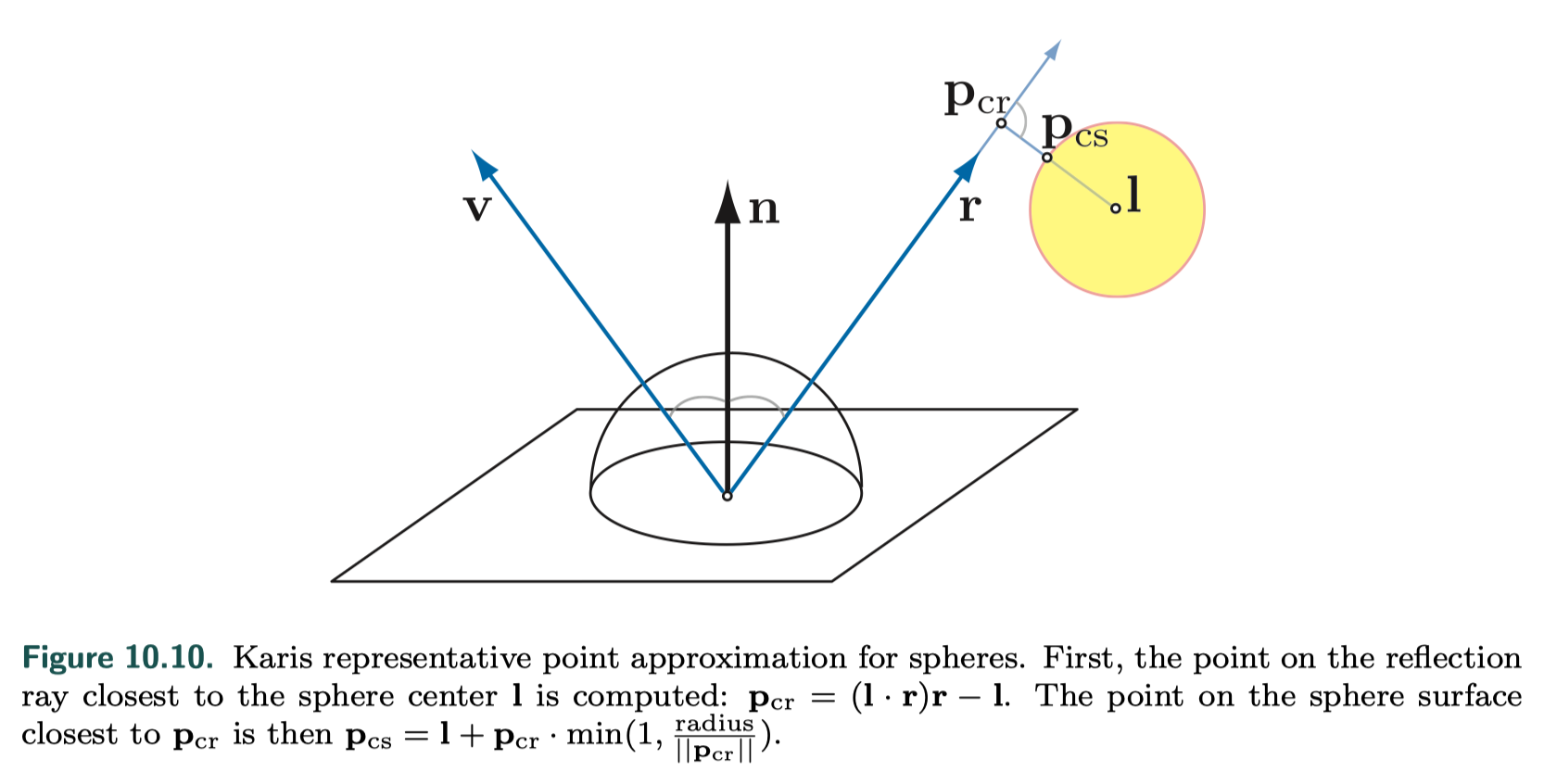
Representative Point Technique

Represent the area illumination’s source with a light direction that changes based on the point being shaded
These approaches resemble the idea of importance sampling in Monte Carlo integration, where we numerically compute the value of a deﬁnite integral by averaging samples over the integration domain. In order to do so more eﬃciently, we can try to prioritize samples that have a large contribution to the overall average.
mean value theorem of definite integrals

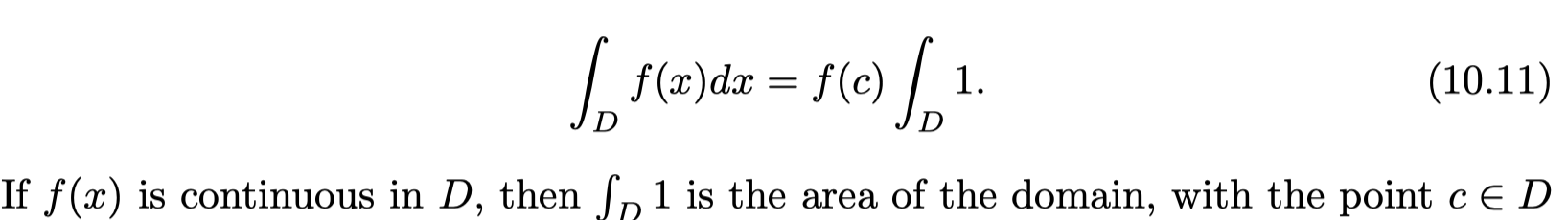
General Light Shapes

tube lights (capsules)

card lights

Drobot, Michal, “Physically Based Area Lights,” in Wolfgang Engel, ed., GPU Pro 5, CRC Press, pp. 67–100, 2014. Cited on p. 116, 388
representative point solution

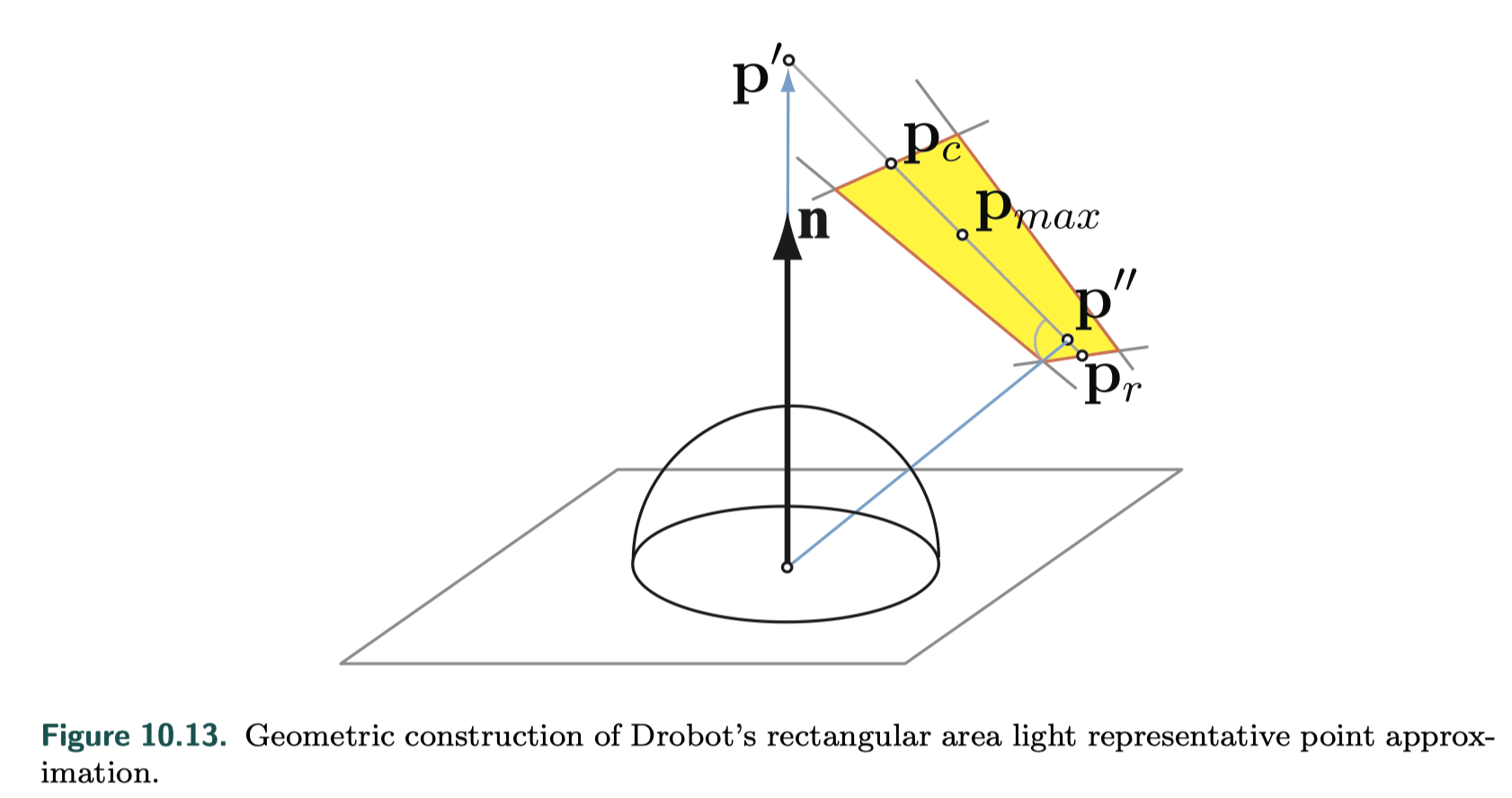
planar polygonal area lights

Heitz, Eric, Jonathan Dupuy, Stephen Hill, and David Neubelt, “Real-Time Polygonal-Light Shading with Linearly Transformed Cosines,” ACM Transactions on Graphics (SIGGRAPH 2016), vol. 35, no. 4, pp. 41:1–41:8, July 2016. Cited on p. 390
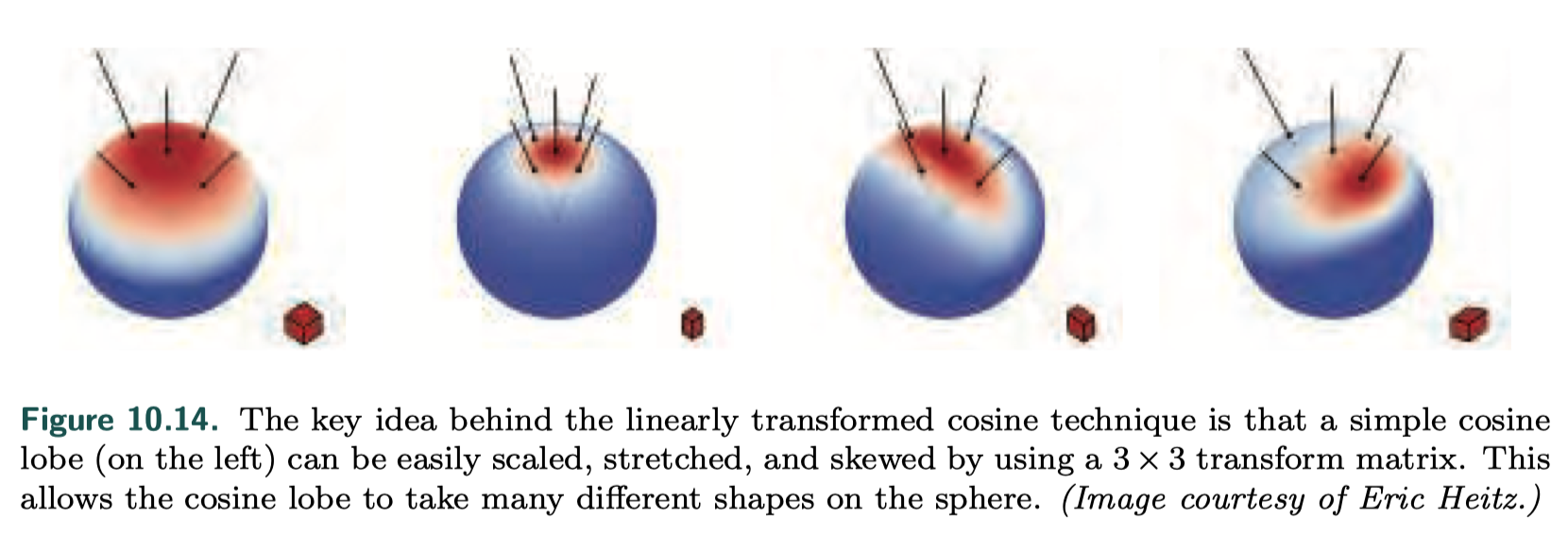
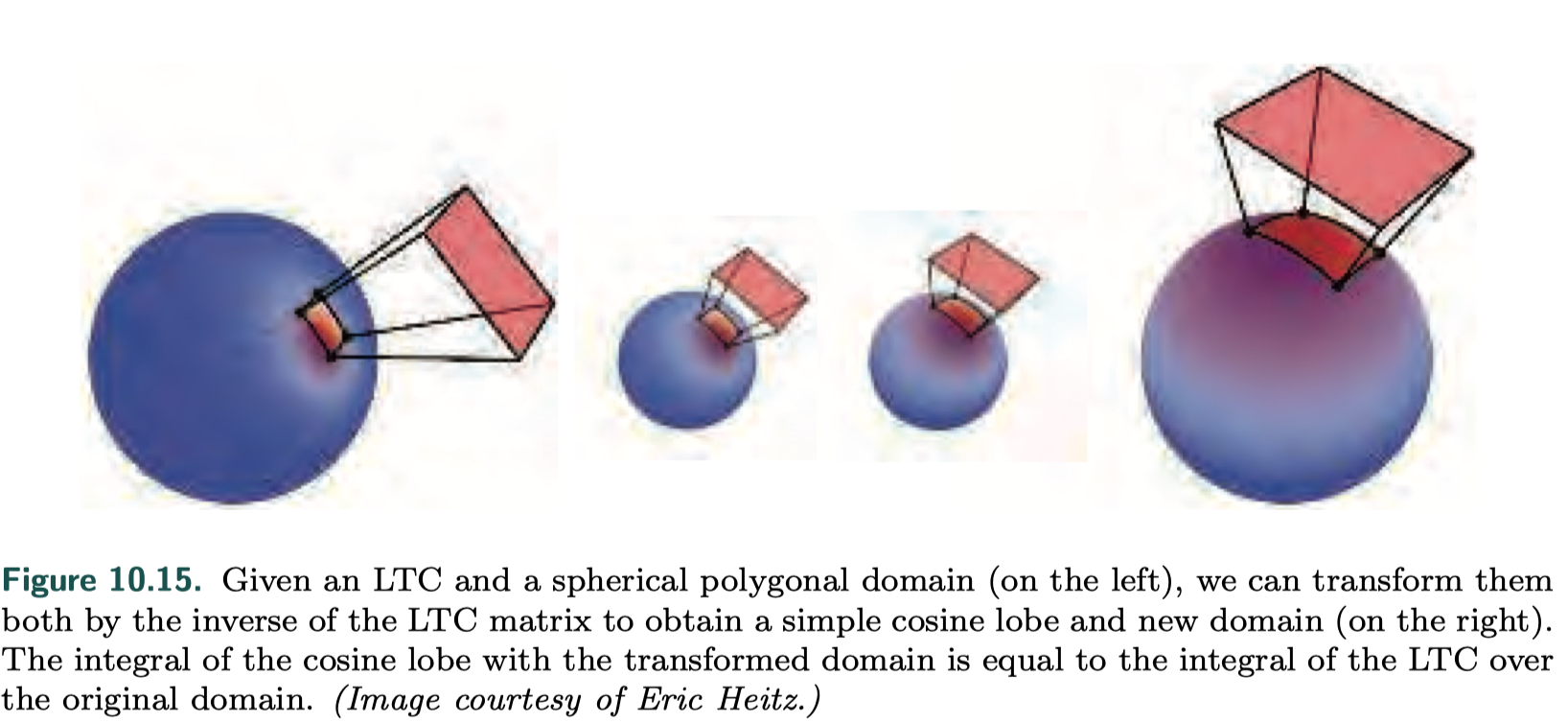
key idea of LTC 把不同的BRDF和simple cosine BRDF做转换

Environment Lighting

Methods to integrate radiance deﬁned by a varying function over all the possible incoming directions.

Ambient Light

the radiance does not vary with direction and has a constant value

Spherical and Hemispherical Functions

spherical bases
properties in a given basis
Simple Tabulated Forms
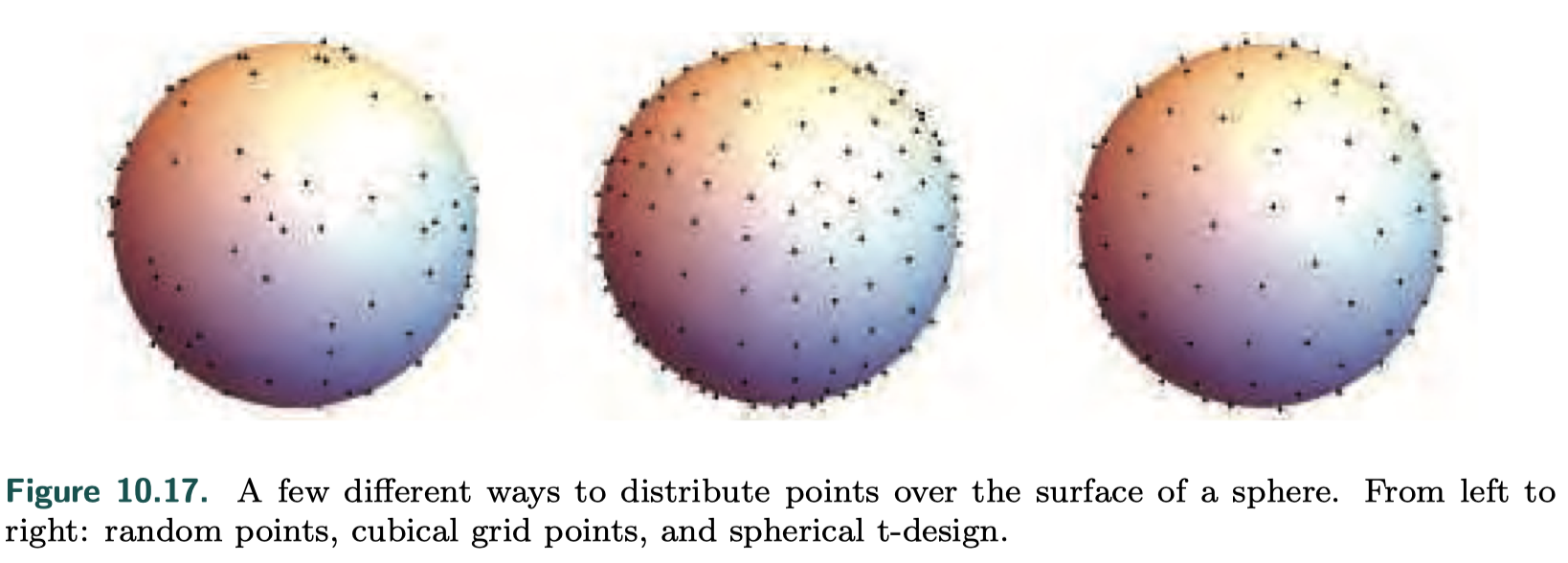
pick several directions and store a value for each
encode many diﬀerent spherical functions with arbitrarily low error by adding more samples as needed
samples to choose

Spherical Bases

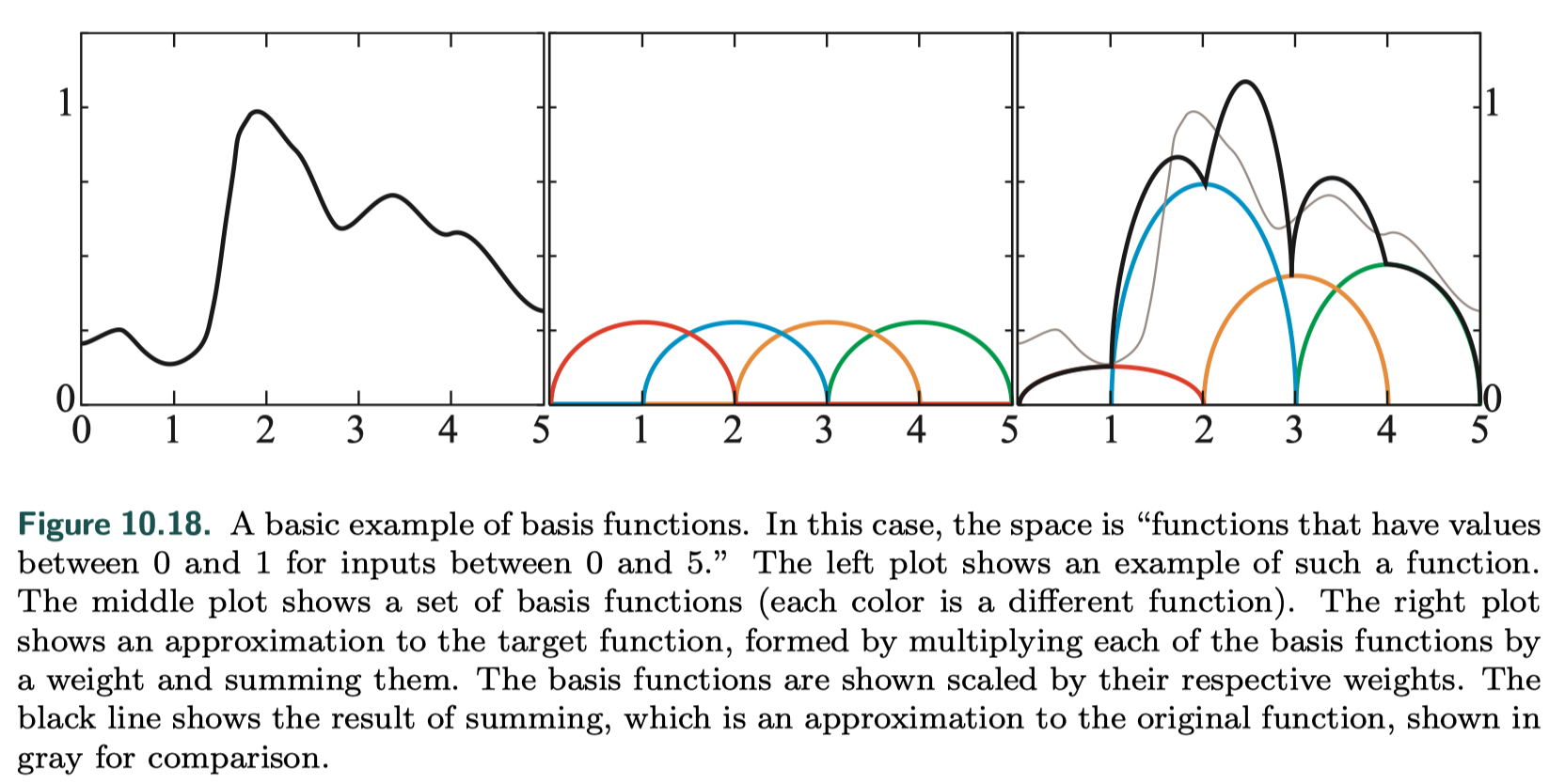
Basic Ideas

ways to project (encode) functions onto representations that use a ﬁxed number of values (coeﬃcients)
basic example
- one kind of most minimal possible base --- constant
- two coefficients
- a more complex example

Spherical Radial Basis Functions

radially symmetric makes the function only one argument
a set of functions called lobes spread across the sphere
projection and reconstruction

Spherical Gaussians

definition
A proper basis is obtained only when we choose a ﬁxed set of lobes (directions and spreads), so that the entire domain is well covered, and perform projection by ﬁtting only the weights w_k.
The optimization problem is formulated as ordinary least-squares optimization.
production and integration
anisotropic spherical guassians

Spherical Harmonics

Spherical harmonics (SH) are an orthogonal set of basis functions over the sphere.
orthogonal means that the inner product of any two diﬀerent functions from the set is zero
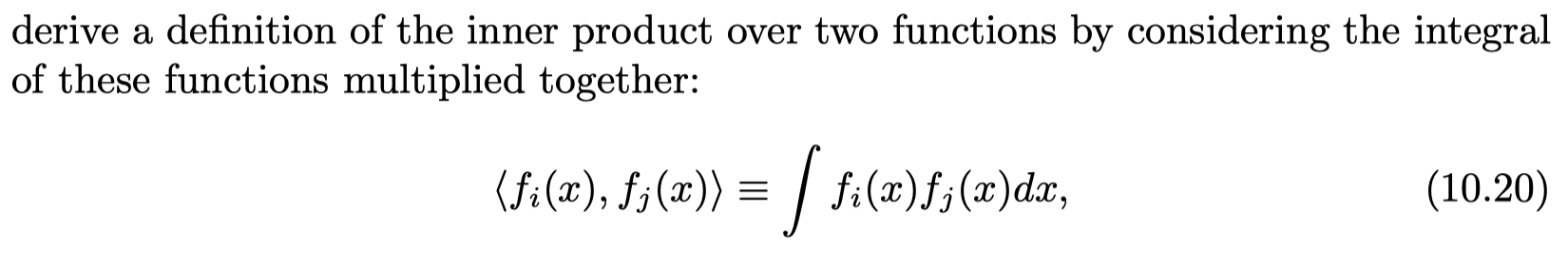
projection
A function space has an inﬁnite number of dimensions, so a ﬁnite number of basis functions can never perfectly represent it.
frequency bands
integral In this spectral domain, the integral of the product of two functions is equal to the dot product of the coeﬃcients of the function projections.

Other Spherical Representations

linearly transformed cosines
spherical wavelets

Hemispherical Bases

half of the signal
the BRDF, the incoming radiance, and the irradiance arriving at given point of an object

Ambient/Highlight/Direction (AHD) Basis

a constant ambient light ---- ambient direction and color
a single directional light that approximates the irradiance in the “highlight” direction ---- highlight direction
the direction where most of the incoming light is concentrated ----- incoming direction and color
projection
- Precomputed Lighting in Call of Duty: Inﬁnite Warfare,” SIGGRAPH Advances in Real-Time Rendering in Games course, Aug. 2017
- signal is ﬁrst projected to spherical harmonics, and the optimal linear direction is used to orient the cosine lobe

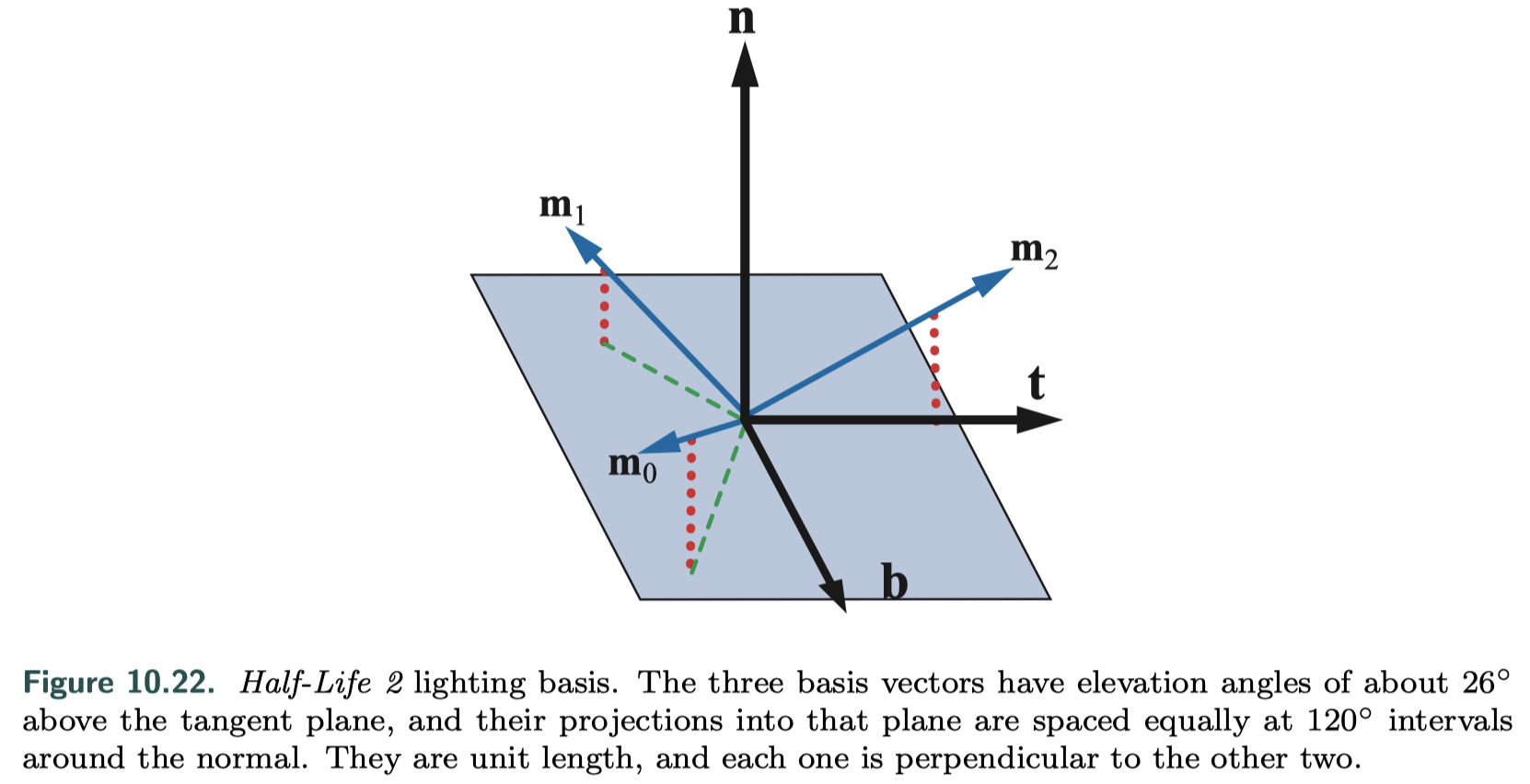
Radiosity Normal Mapping/Half-Life 2 Basis

represents hemispherical functions on surfaces by sampling three directions in tangent space
projection and reconstruction

Hemispherical Harmonics(HSH)/H-Basis

Zernike polynomials
H-basis
- Habel, Ralf, and Michael Wimmer, “Eﬃcient Irradiance Normal Mapping,” in Proceedings of the 2010 ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games
- take part of the spherical harmonic basis for the longitudinal parameterization and parts of the HSH for the latitudinal one

Environment Mapping

Definition

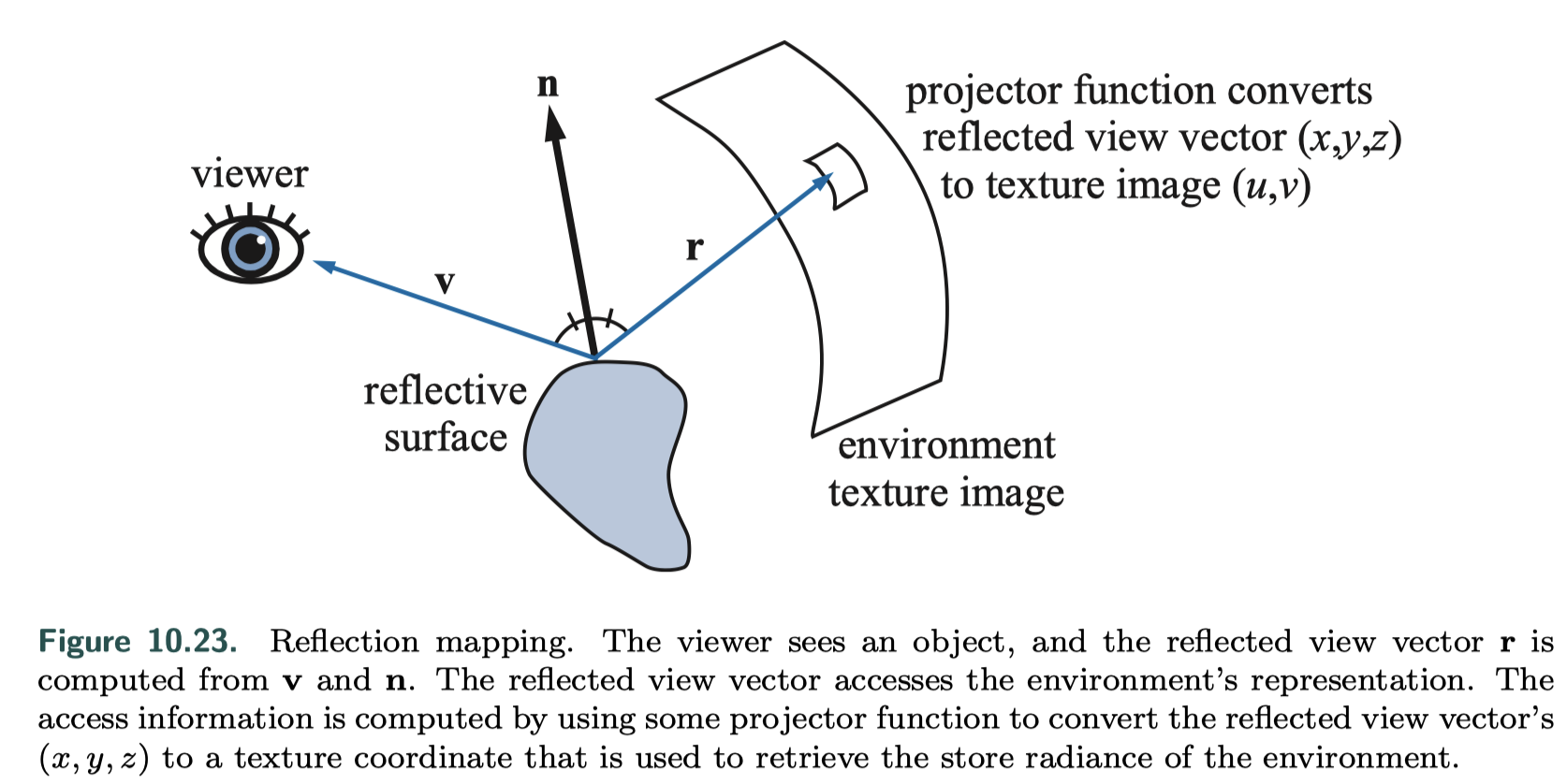
Recording a spherical function in one or more images is called environment mapping, as we typically use texture mapping to implement the lookups in the table.
How well we can integrate environment lighting with given materials.
A variety of projector functions that map the reﬂected view vector into one or more textures.

Reﬂection mapping

assume that the BRDF is a perfect mirror
calculation

Mapping

Latitude-Longitude Mapping

spherical coordinates ( ρ , φ ). Here φ , equivalent to the longitude, varies from 0 to 2π radians, and ρ , the latitude, varies from 0 to π radians.
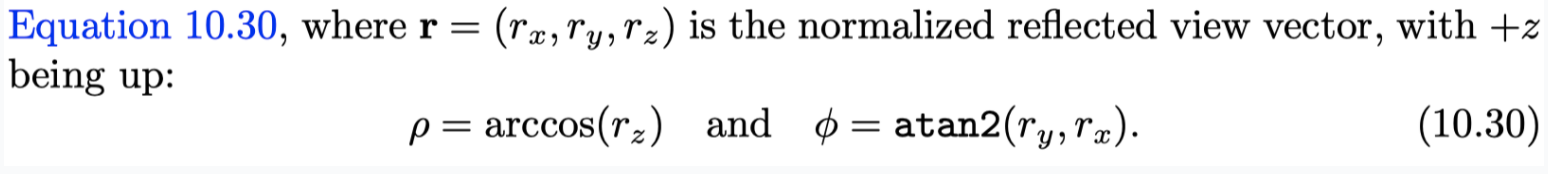
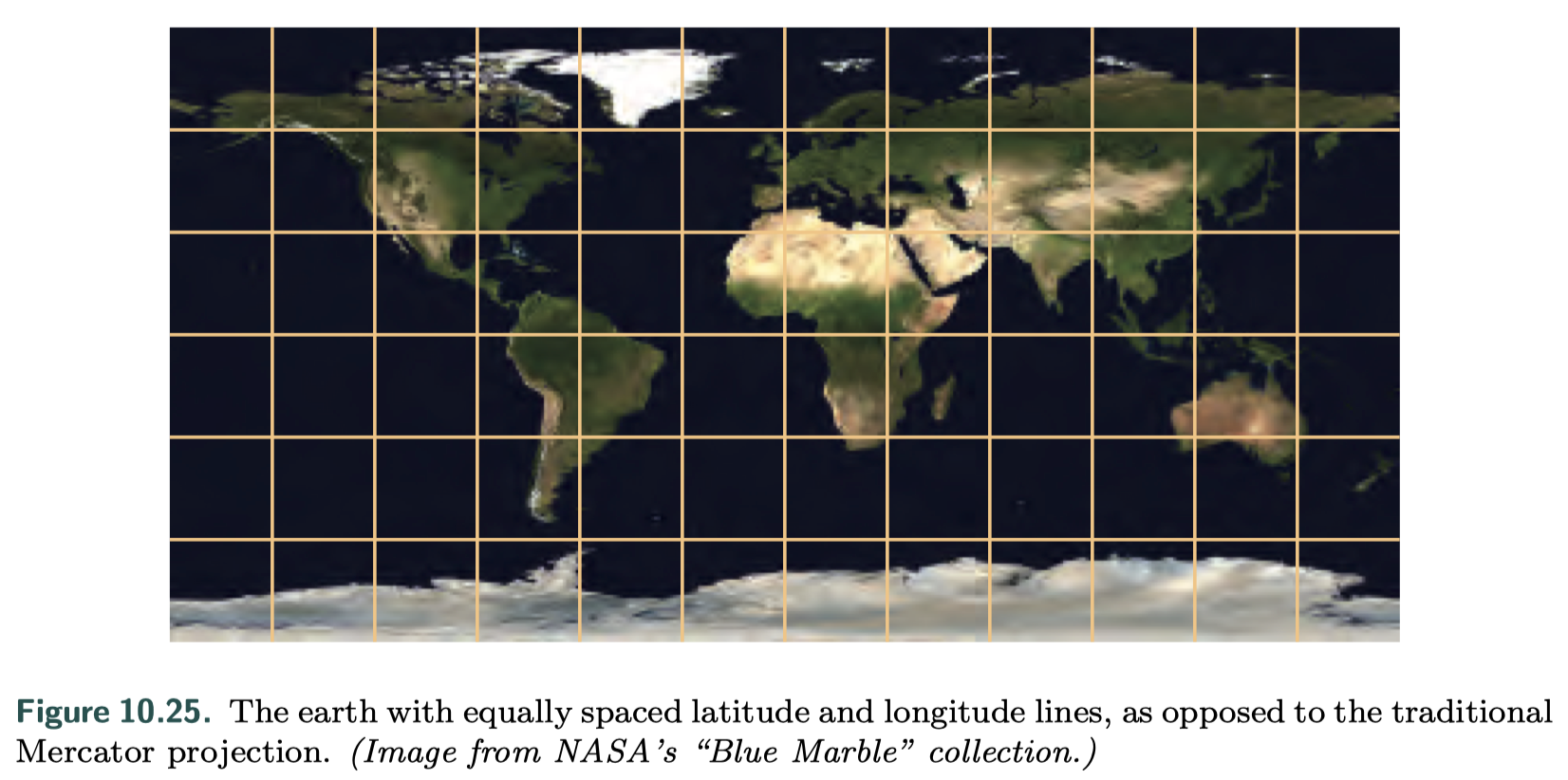
problem
- the density of information is nowhere near uniform
- the areas near the poles receive many more texels than those near the equator
- result in artifacts when employing hardware texture ﬁltering especially visible at the two pole singularities
- transcendental functions such as arccosine are costly on GPUs

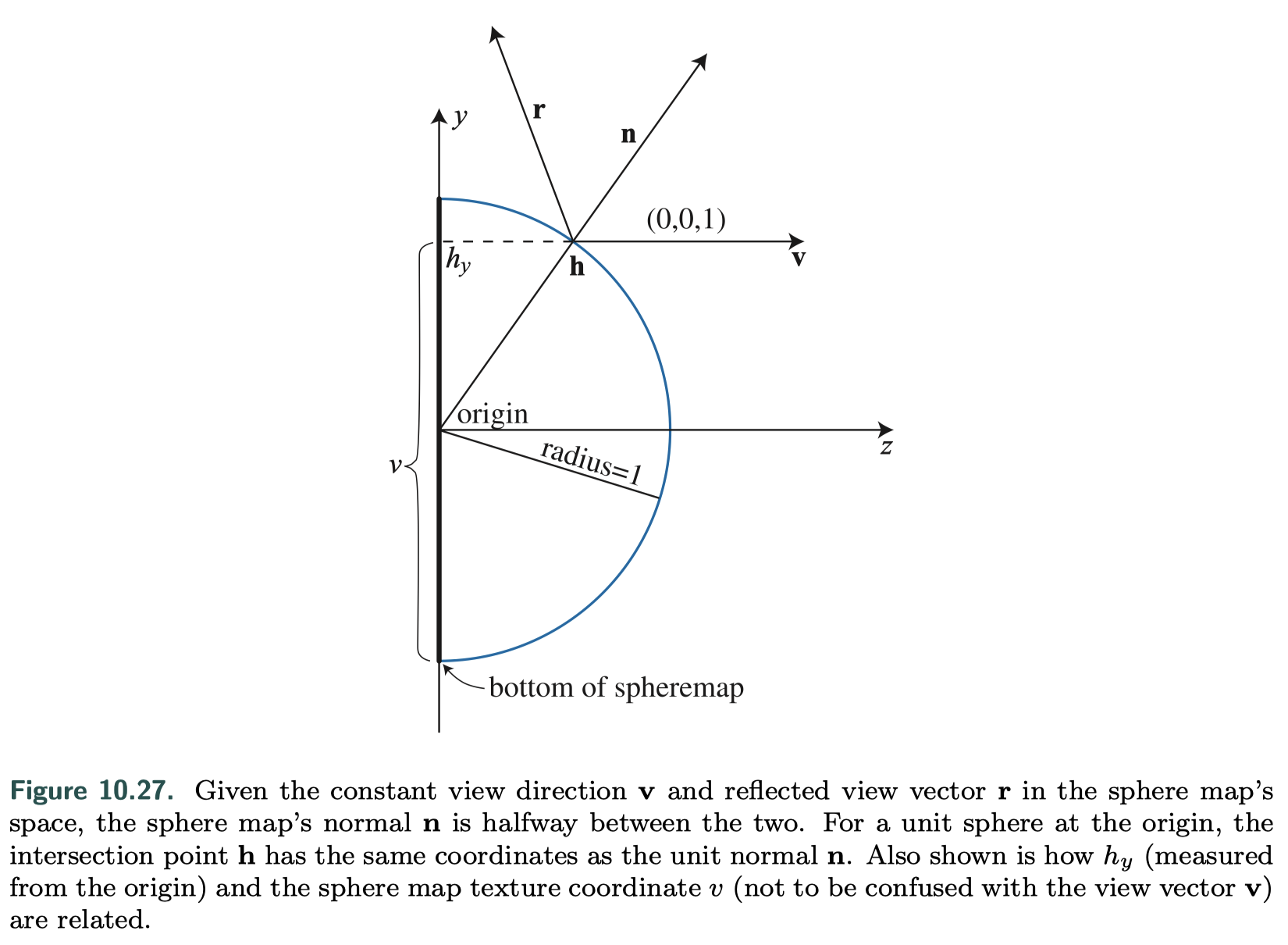
Sphere Mapping

in sphere map's space, view vector is always (0, 0, 1)
maps each reﬂected view direction to a point on the two-dimensional image of this sphere
derive the surface normal(view space) on the sphere, which will then yield the (u, v) parameters needed to access the sphere map
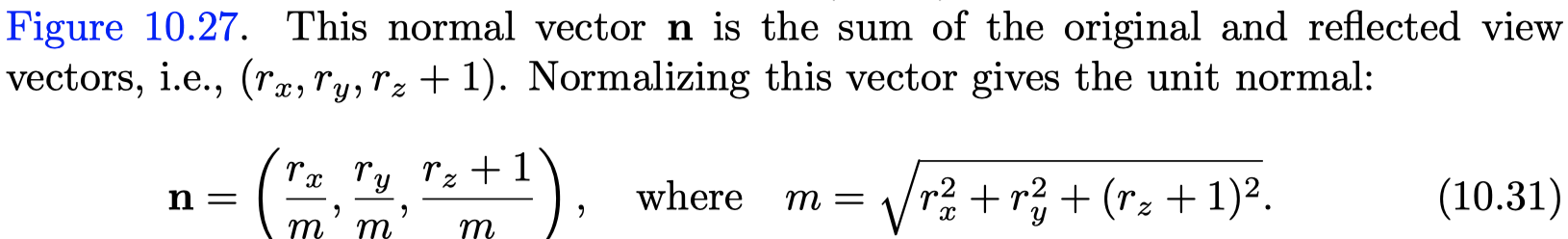
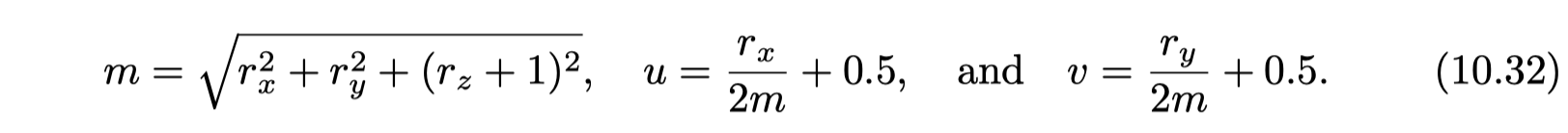
much simpler to compute
one singularity located around the edge of the image circle
valid for only a single view direction

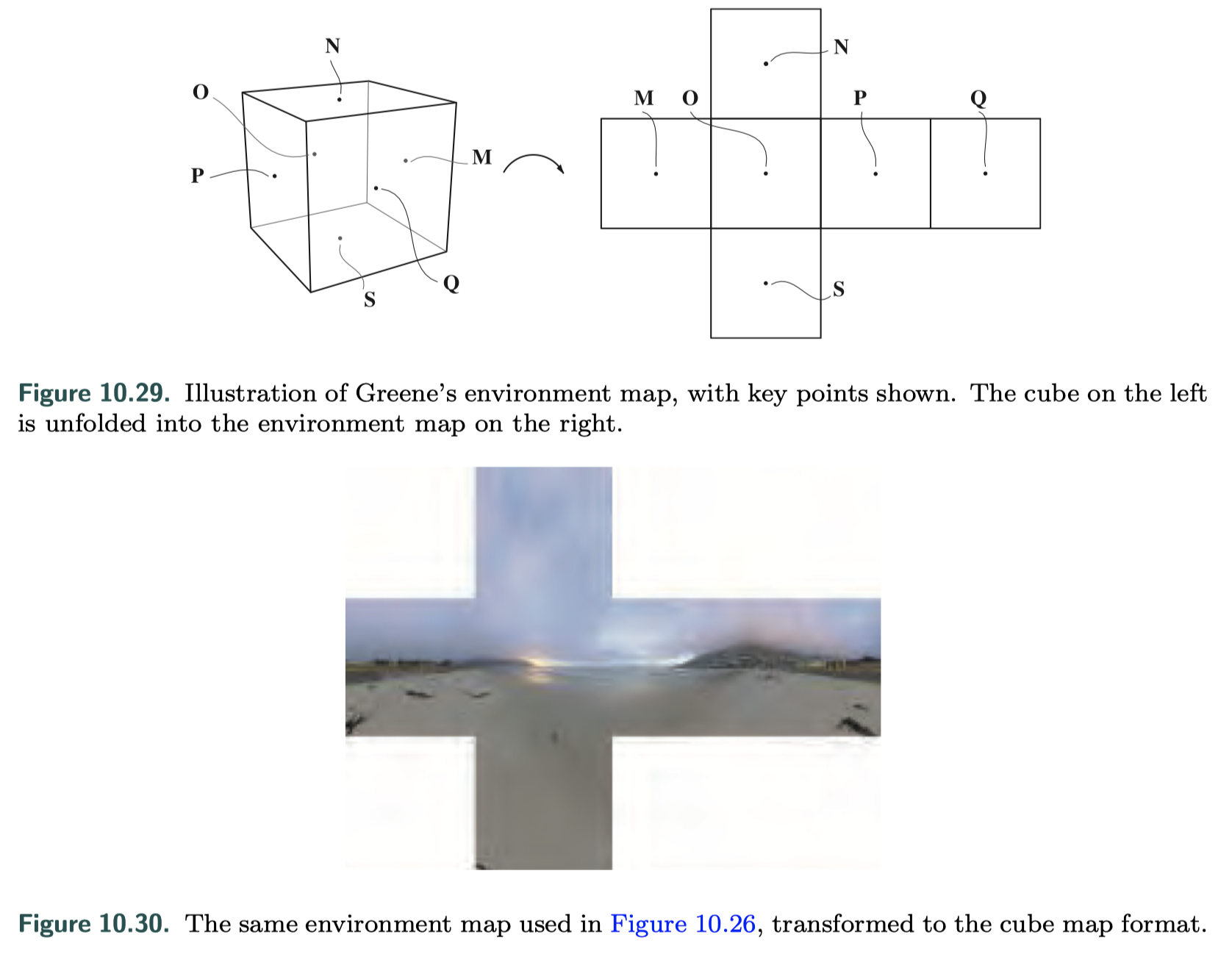
Cube Mapping

created by projecting the environment onto the sides of a cube positioned with its center at the camera’s location
its projection is implemented directly in hardware on modern GPUs
view-independent
much more uniform sampling characteristics
modern GPUs can now correctly perform this ﬁltering across edges

Other Projections

dual paraboloid environment mapping
- more uniform texel sampling of the environment compared to the sphere map and the cube map
- take care for proper sampling and interpolation at the seam between the two projections which is expensive
Octahedral(八面体) mapping
- projection Given a reﬂection direction r
  - no ﬁltering issues as the seams of the parameterization correspond with the edges of the texture used
Radially-Symmetric Reﬂection Maps
- a simple factorization using a single one-dimensional texture storing the radiance values along any meridian line from the symmetry axis

Specular Image-Based Lighting

Ideas

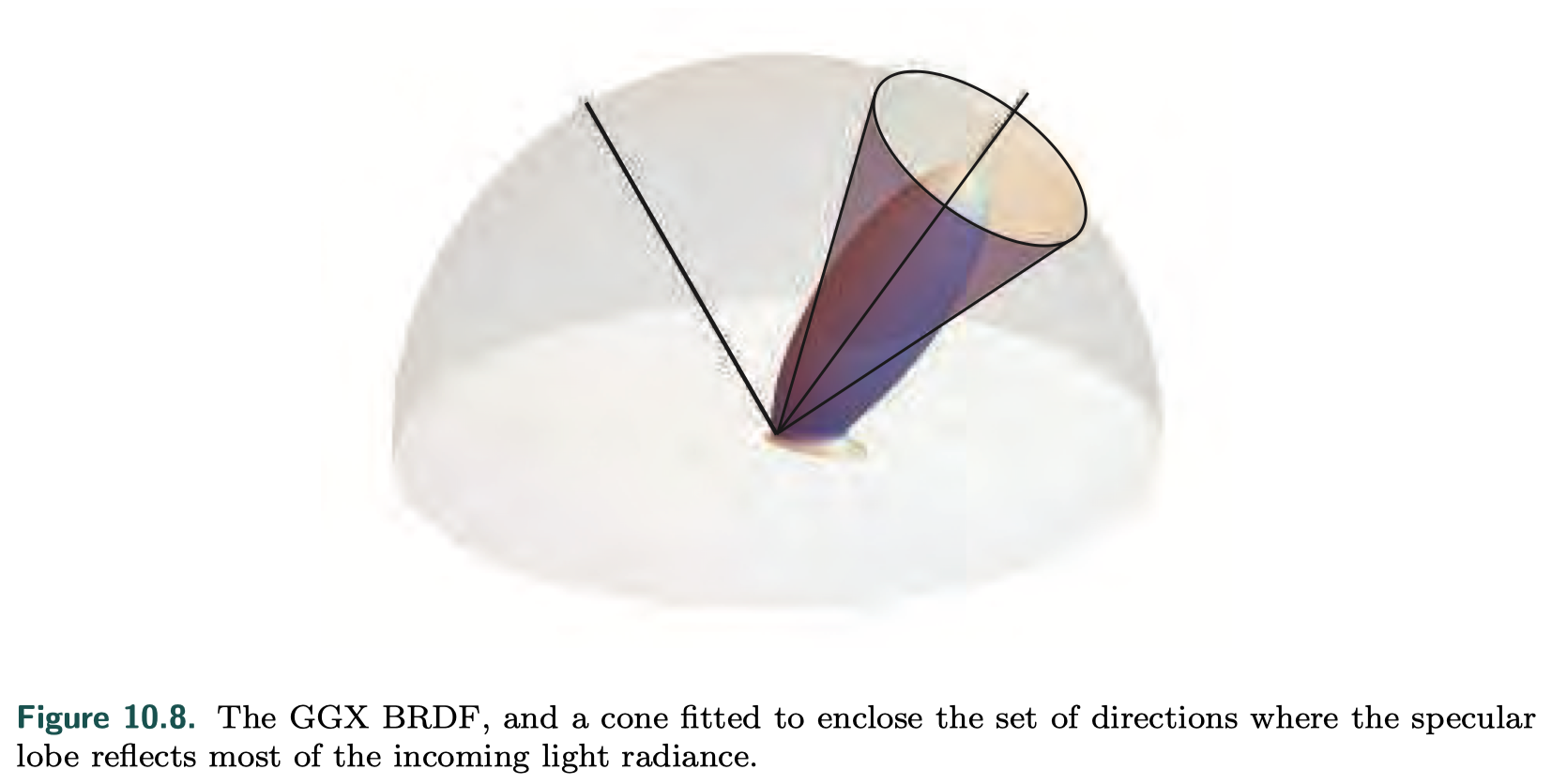
blurring the environment map texture to simulate surface roughness
consider the shape a BRDF function at least ﬁve dimensions of input values (roughness and two polar angles each for the view and normal directions) that control the resulting lobe shape
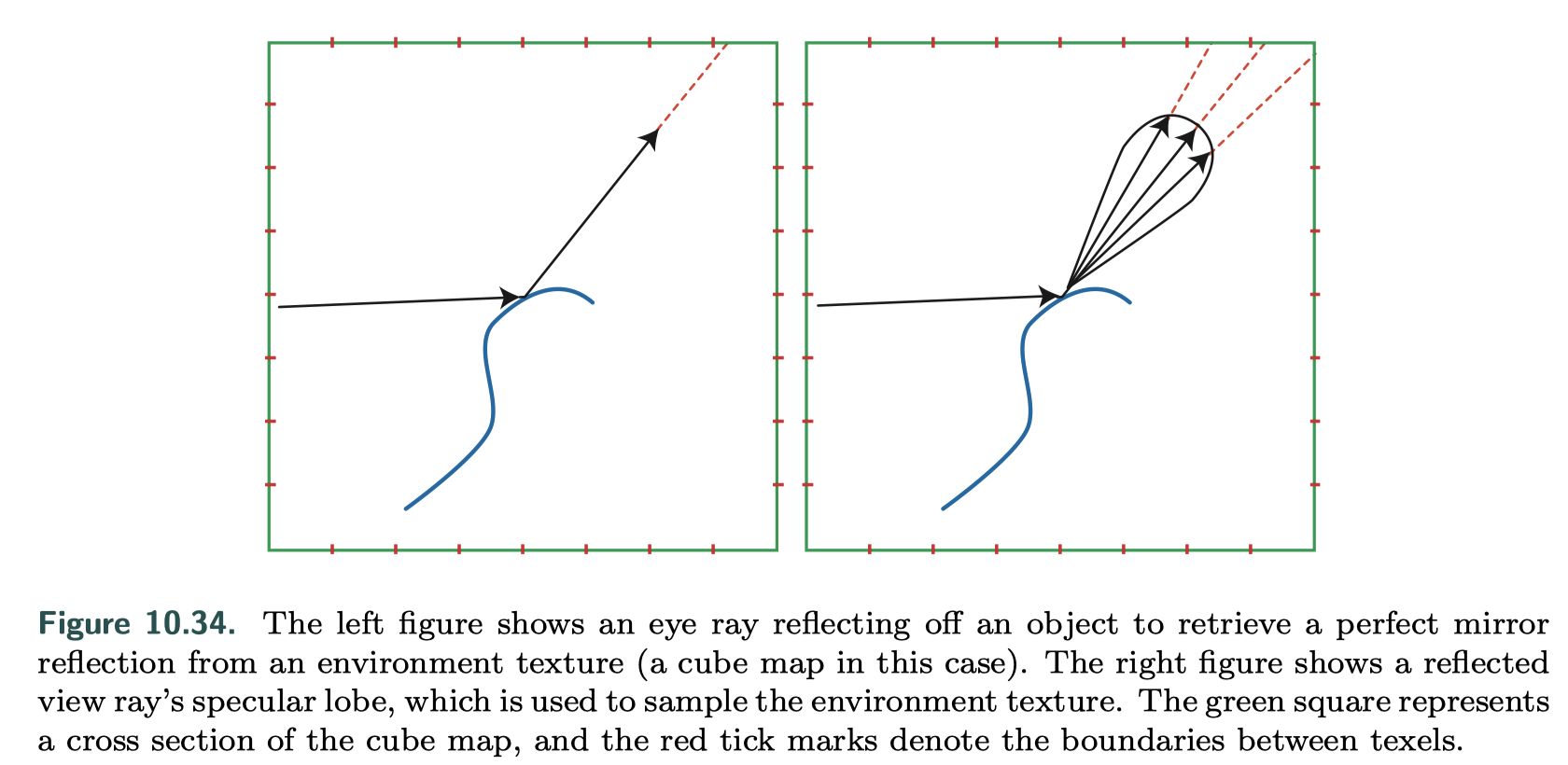
indexed with the reﬂected view vector which contain radiance values

Preﬁltered Environment Mapping

To accommodate for diﬀerent roughness levels, it is common to employ the mipmaps of an environment cube map. Each level is used to store blurred versions of the incoming radiance, with higher mip levels storing rougher surfaces.

Convolving the Environment Map

Split-Integral Approximation for Microfacet BRDFs

many techniques have been developed to lessen the BRDF approximation issues inherent in cube map preﬁltering
split-integral approximation
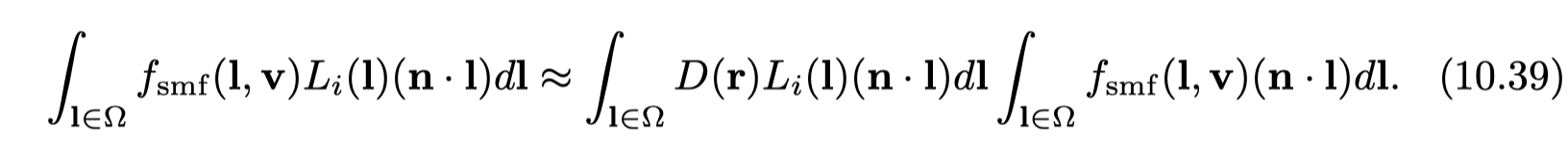
- the ﬁrst depends only on surface roughness and the reﬂection vector, with the assumption of a radial symmetric D lobe
  - in practice, we can use any lobe, imposing n = v = r
- the second integral is the hemispherical-directional reﬂectance of the specular term
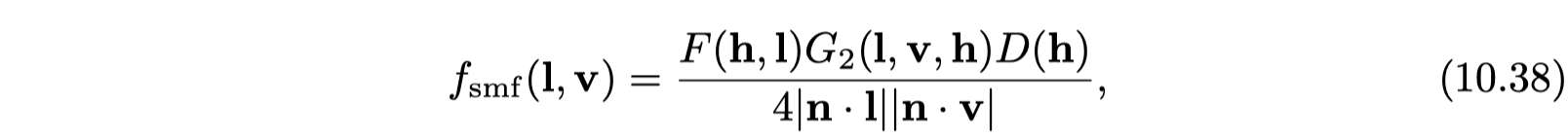
  - depends on the elevation angle θ, roughness α, and Fresnel term F (F0)

Asymmetric and Anisotropic Lobes

uses a single sample, but tries to ﬁnd the best lobe to approximate the BRDF in the current view direction instead of relying on a constant correction factor
- better simulates surfaces at grazing angles
averages several samples from diﬀerent lobes
- include the stretched highlights typical of half-vector models

Irradiance Environment Mapping

indexed with just the surface normal n, and they contain irradiance values
for each texel in the map, we need to sum up the cosine-weighted contributions of all illumination aﬀecting a surface facing in a given normal direction
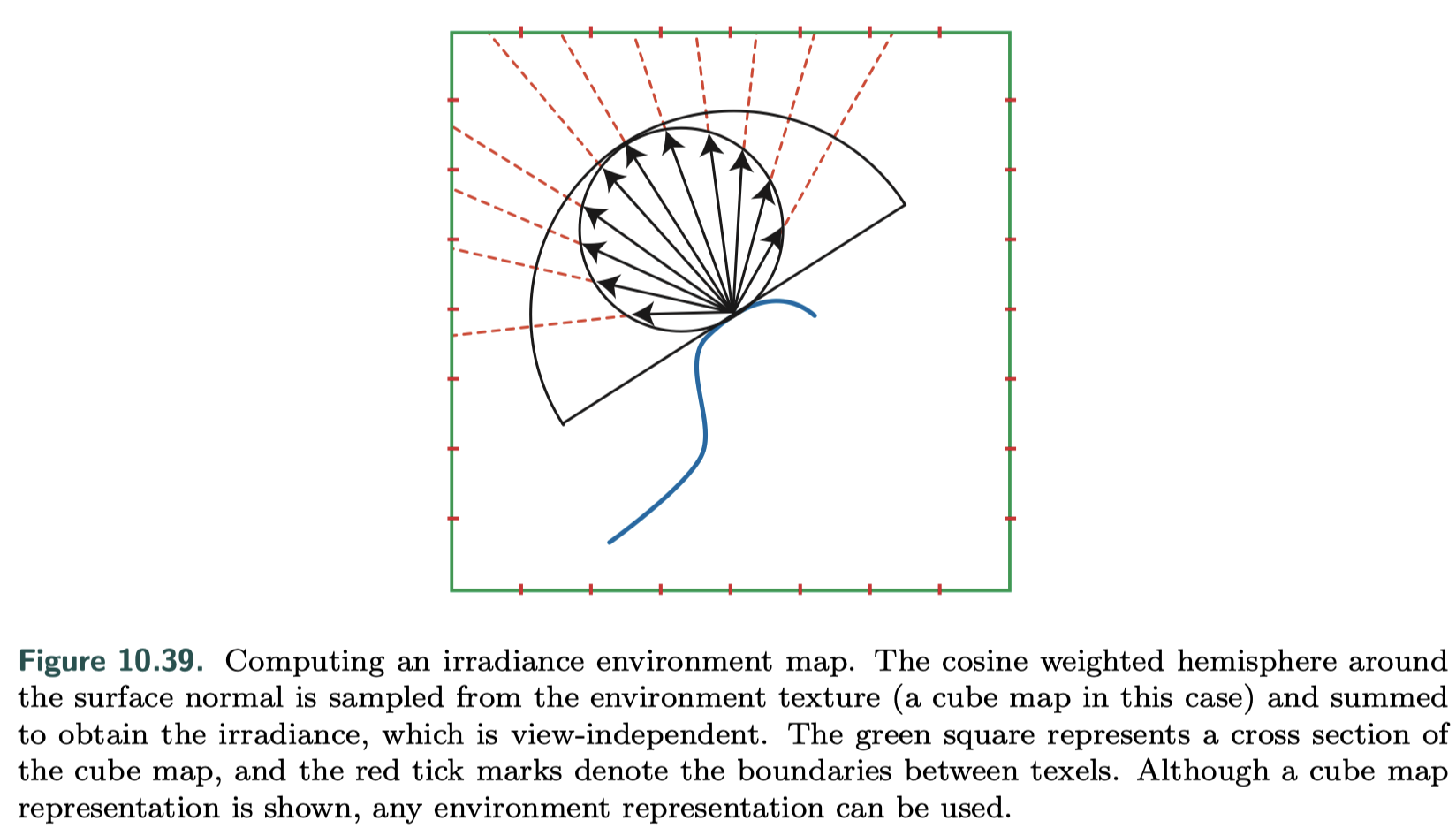
stored and accessed separately from the specular environment or reﬂection map, usually in a view-independent representation such as a cube map

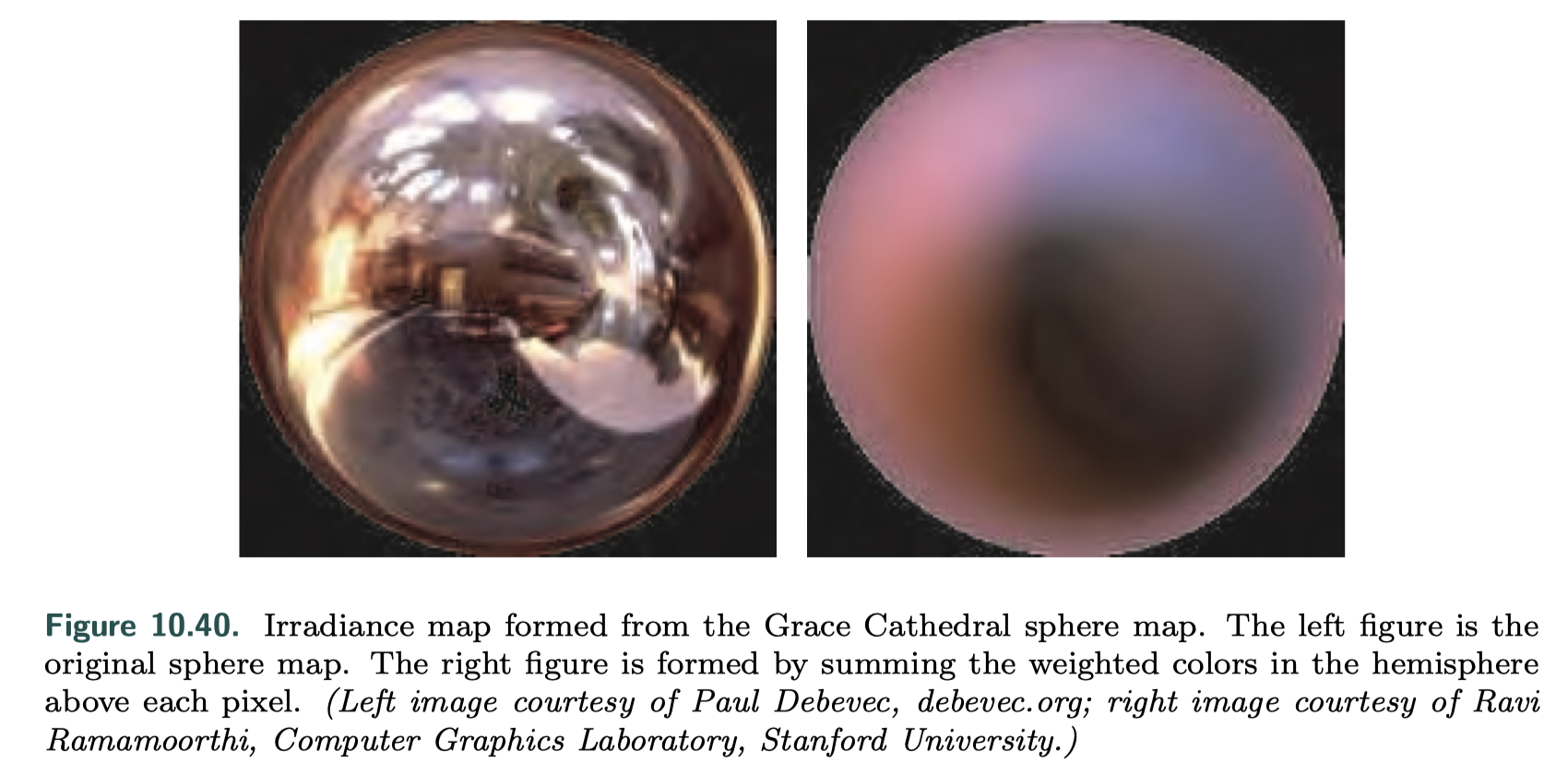
Spherical Harmonics Irradiance

cause irradiance from environment lighting is smooth
convolving radiance with a cosine lobe results in the removal of all the high-frequency components from the environment map
an accuracy of about 1% with just the ﬁrst nine SH coeﬃcients (each coeﬃcient is an RGB vector, so we need to store 27 ﬂoating point numbers)
SH projection
dynamic light sources can be added into an existing SH irradiance environment map

Other Representations

many irradiance environment maps have two dominant colors: a sky color on the top and a ground color on the bottom
hemisphere lighting model
- the upper hemisphere is assumed to emit a uniform radiance L_sky
- the lower hemisphere is assumed to emit a uniform radiance L_ground where θ is the angle between the surface normal and the sky hemisphere axis
a faster approximation
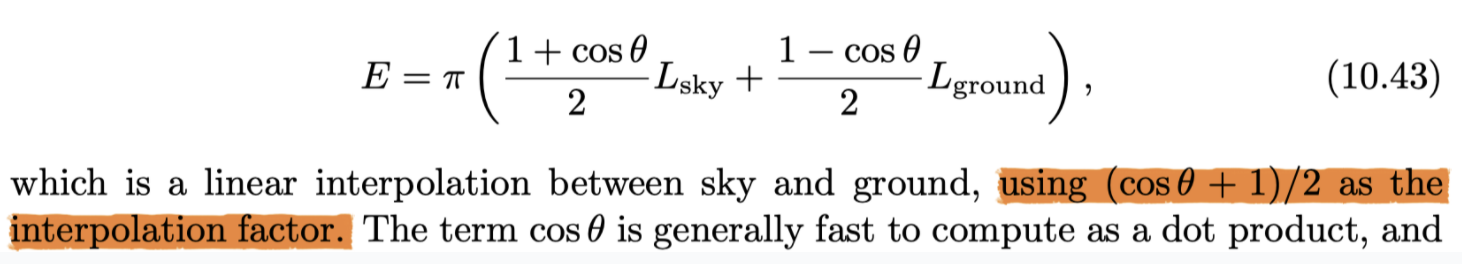
wavelet representations

Sources of Error

employing a mix of techniques for lighting means that we are working with approximations BRDF model that have varying degrees of error
make sure that the discrepancies between diﬀerent forms of lighting are not evident
occlusions are also of key importance for realistic rendering, as light “leaking” where there should be none is often more noticeable than not having light where it should be
assume inﬁnitely distant radiance sources, ones that are never possible
assume the lights emit radiance uniformly over the outgoing hemisphere for each point on their surface